Juan Báez Ibarra (*)
Con esta lección (1/3) iniciaremos el estudio de las Matemáticas de los Bonos con la identificación de los componentes básicos de un bono.
Además realizaremos y comprenderemos los cálculos de valor futuro y valor actual de un solo flujo de fondos.
Componentes Básicos de un Bono
El Valor Par o Valor Nominal es el monto o volumen de capital del bono.
La Tasa del Cupón es el porcentaje estipulado del valor nominal que se abona anualmente al tenedor del bono. El valor nominal y la tasa del cupón se multiplican para calcular el monto en dólares de estos pagos anuales de cupón.
El Vencimiento o Plazo es el tiempo que transcurre hasta que se devuelve el capital al tenedor del bono.
El precio es el precio corriente de mercado del bono.
El Rendimiento al Vencimiento (RAV) es el rendimiento para el inversor que paga el precio corriente de mercado por el bono y lo mantiene en cartera hasta su vencimiento.
El Valor Tiempo del Dinero
Antes de poder comprender plenamente los modelos de fijación de precio para los bonos y las mediciones de rendimiento, necesitamos entender el valor tiempo del dinero.
Aquí se repasarán dos conceptos: el Valor Futuro y el Valor Actual. La idea de que el valor del dinero está vinculado al tiempo se relaciona con el hecho de que se puede invertir a alguna tasa de interés.
Valor Futuro (FV)
Intuitivamente, todos sabemos que un dólar que se invierte hoy tendrá más valor en el futuro. Esto es así porque podemos ganar un interés sobre ese dólar. Al calcular el Valor Futuro (FV) de una inversión, debemos considerar una serie de factores.
Específicamente, necesitamos conocer la tasa de interés que se está pagando y el tiempo durante el cual el capital estará invertido. También necesitamos saber con qué frecuencia se capitaliza el interés.
Si el valor futuro de una inversión se calcula al final de un determinado período sin capitalización de intereses, se denomina de Interés Simple. En la ecuación (3-1), si el capital, P, se invierte durante un año a una tasa de interés i, el valor futuro se calcula de la siguiente manera:
(3.1) FV = P (1 + i)
Si la inversión se mantiene durante varios períodos y se calcula el interés al final de cada período sobre el capital y el interés devengado, lo llamamos Interés Compuesto.
El valor futuro de una inversión, P, mantenida durante n períodos, en la que cada uno da un interés a la tasa i por período, se calcula de la siguiente manera.
(3-2) FV = P (1 + i)
Una complicación más a los cálculos del FV implica el pago de interés más de una vez por período. Por ejemplo, los bonos del Tesoro estadounidense realizan pagos de cupón dos veces por año. Si la tasa del cupón es 8%, sobre un valor nominal de U$S1000, el tenedor del bono recibirá dos pagos de cupón de U$S40 por año.
Debido a que el primer pago se puede reinvertir a una tasa de interés, el rendimiento real para el tenedor del bono, suponiendo que el bono se compró a la par, será mayor que 8%. En esta sección, analizaremos específicamente los bonos que pagan cupones semestrales.
Usted ya ha completado la primera parte de esta sección. Ahora, ya debe saber qué significa el concepto de valor tiempo del dinero. En los cálculos de valor futuro, ha observado que el FV de una inversión es una función positiva del capital, plazo de vencimiento y tasa de interés.
Valor Actual (PV)
Ahora que ya comprende el concepto de valor futuro, volvamos atrás para calcular el valor actual de un determinado valor en el futuro. El valor actual (PV) es el monto que se debe invertir hoy a una tasa de interés determinada a fin de realizar un determinado monto en el futuro.
El proceso de resolver el valor actual de una corriente futura de flujo de fondos se conoce como proceso de descuento. La tasa de interés que se utiliza para esto se conoce como tasa de descuento.
Más aun, la tasa de descuento que pone en ecuación el PV de una corriente de flujo de fondos futura respecto de su Precio de Mercado corriente se conoce como Rendimiento al Vencimiento (RAV). Analizaremos esta medida de rendimiento así como también otras en más detalle, más adelante.
Supongamos que usted tiene una oportunidad de inversión que le pagará U$S1.000 a un año. Dada una tasa de interés de mercado positiva, esperaría pagar menos de U$S1.000 hoy por esa oportunidad. Esto se debe a que su capacidad para invertir dinero hoy le permitiría a usted ganar un interés tal que el FV de su inversión sea mayor a su inversión inicial.
La fórmula del valor actual deriva de la fórmula de valor futuro que se presentó anteriormente. A continuación, se repite la ecuación (3-2).
(3-2) FV = P (1 + i)
En esta fórmula, recuerde que P representa el capital que se invirtió inicialmente. Resolviendo P, obtenemos una expresión para el Valor Actual del flujo de fondos futuro, o del capital que tendríamos que haber invertido a la tasa i a fin de realizar el FV al vencimiento. Así, obtenemos la siguiente expresión:
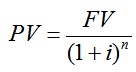
Donde P fue reemplazado por PV.
En estos problemas, note que hay un solo flujo de fondos asociado a la inversión. La fórmula para el PV de una corriente de flujo de fondos es apenas levemente más complicada y se analiza a continuación.
(*) Dr. Juan Báez Ibarra – Máster y Doctor en Contabilidad por la Fundación Getulio Varga (FGV) y Universidad de San Pablo (USP) del Brasil, respectivamente. Instructor nacional e internacional de Riesgos Financieros, Productos y Mercados Financieros, NIIFs, ALD y Gestión Integral de Riesgos. Amplia experiencia en Entidades Financieras.