Juan Báez Ibarra (*)
En esta lección (2/3) estudiaremos temas como la Anualidad, Como calcular el Valor Actual usando la calculadora financiera y concluimos la lección con la determinación del Precio de un Bono.
Anualidad
Cuando periódicamente se paga el mismo monto en efectivo al inversor, se denomina anualidad. A los fines de este análisis, supondremos que los flujos de fondos se pagan todos al final de cada período. En este caso, la anualidad se conoce como anualidad ordinaria.
Para calcular el valor actual de una anualidad, debemos descontar cada uno de los distintos flujos de fondos y luego agregar los valores presentes de todos los flujos de fondos juntos. La fórmula siguiente ilustra el cálculo del PV de una anualidad, donde el flujo de fondos constante, o pago, es PMT, e i es la tasa de descuento.
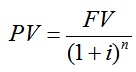
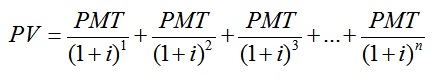
Esta fórmula se puede replantear de la siguiente manera:
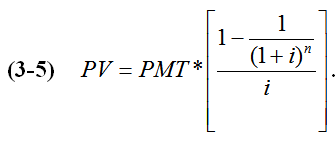
Nota – Cálculo de anualidades con calculadora financiera (Hewlett-Packard 12C o 17B)

Con varios flujos de fondos, utilizar la función yx de una calculadora llevaría mucho tiempo. La calculadora financiera facilita mucho más el proceso.
Bonos como Títulos de renta fija
Muchos instrumentos de renta fija requieren de un egreso de fondos inicial y, a su vez, ofrecen un retorno periódico en efectivo en la forma de un pago de cupón, así como también el retorno del capital a una fecha final de vencimiento.
Los títulos de renta fija son simplemente una anualidad más un flujo de fondos adicional que es el retorno del capital del inversor o Par. A fin de determinar el Valor Actual de un instrumento de estas características, uno debe determinar el valor actual de todos los flujos de fondos y sumarlos a todos de la siguiente manera:
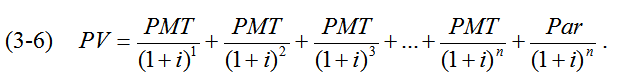
El precio de un bono no es más que su valor actual. Como se verá en mayor detalle más adelante, la tasa de descuento, i, que se utiliza para calcular el valor actual es el Rendimiento al Vencimiento del bono. La ecuación de PV se simplifica de la siguiente manera:
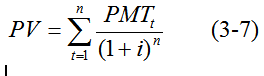
Donde PMTt es igual al pago de cupón para los períodos comprendidos entre 1 y n y es igual al pago de cupón más el valor nominal del bono en el período t.
Observe el caso especial de un Bono con Cupón Cero. Un bono con cupón cero no da pagos de cupón y se vende a descuento de su valor nominal. Al vencimiento, el inversor recibe el valor nominal del bono. Vale la misma fórmula, la ecuación 3-6, para el valor actual de un título de renta fija, pero es mucho más fácil de resolver ya que es un solo flujo de fondos. Todos los períodos PMT equivalen a cero. El único plazo aplicable es el último, así se utiliza la formula de Valor Actual,
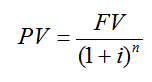
Ejemplo numérico: valoración de bonos (con cupones)
Usted desea valorar un bono con un cupón anual de 7% y tres años más hasta su vencimiento.
El valor nominal del bono es $100, y la tasa de mercado disponible para bonos recién emitidos comparables es 10%.
¿Cuál es el valor actual del bono? Explique la intuición detrás del número que ha calculado.
Solución:
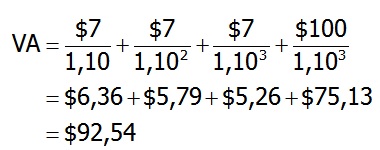
Intuición: si tuviera $92,54 disponibles hoy y los invirtiera a 10%, podría obtener valores futuros iguales a los flujos de efectivo que ofrece este bono, o sea recibir cada cada uno de los tres años $ 7 (cupones) y además en el año tres recibir $ 100 (Valor Par)
Ahora hágalo usted…
Suponga que la tasa de interés para bonos recién emitidos comparables disminuye a 5%.
- ¿Cuál es el nuevo Valor Actual de este bono?
$105,45
Nota: Cuando la tasa de interés del mercado (RAV)
bajó, el valor actual (precio) del bono subió.
Que pasa si la tasa de descuento i Aumenta al 12%
El valor actual (precio) del bono cayó a
$ 87,95
(*) Dr. Juan Báez Ibarra – Máster y Doctor en Contabilidad por la Fundación Getulio Varga (FGV) y Universidad de San Pablo (USP) del Brasil, respectivamente. Instructor nacional e internacional de Riesgos Financieros, Productos y Mercados Financieros, NIIFs, ALD y Gestión Integral de Riesgos. Amplia experiencia en Entidades Financieras.