Juan Báez Ibarra (*)
En este artículo, última parte del estudio de las Matemáticas de los Bonos, veremos la relación que existe entre Precio y Rendimiento, el importante concepto de la TIR o la Tasa de Rendimiento al Vencimiento (RAV) y su utilización para valorar o calcular el valor presente o actual de un bono.
Relación (complicada) entre Precio-Rendimiento
En el análisis anterior, usted se familiarizó con los conceptos de Valor Futuro y Valor Actual y como la modificación del Rendimiento al Vencimiento (RAV) afecta el Valor Actual o Precio del Bono. En esta sección, aplicaremos estos conceptos para comprender el comportamiento de los títulos de renta fija.
Antes de enumerar estas características, aclaremos un término: Rendimiento al Vencimiento (RAV). En las ecuaciones 3-6 y 3-7, usted utilizó una tasa de descuento constante en el denominador para realizar la ecuación del PV de los flujos de fondos al precio del bono. Esta tasa de descuento constante se denomina Rendimiento al Vencimiento (prometido).
Y hagamos ahora un pequeño paréntesis para recordar algunos conceptos que ya manejamos en los cursos de graduación principalmente en las disciplinas de Matemática Financiera, Proyecto de Inversión, Finanzas, ahí te habrás familiarizado con la TIR (Tasa Interna de Retorno).
Recuerdas la definición de la TIR: es la tasa de interés que iguala el Valor Actual de los Flujos Futuros con la Inversión Inicial en el Proyecto. Y a este nuestro bien conocido TIR en la jerga financiera se le llama Rendimiento al Vencimiento (RAV).
Aplicado a las Matemáticas de los Bonos, La TIR o el RAV es la tasa de interés de mercado que iguala el Valor Actual de los Flujos Futuros en concepto de cupones y devolución del principal con el Precio de Mercado del Bono.
Continuando, de algunos de los cálculos que usted ya realizó más arriba, ya debe de haber comenzado a inferir que el precio de un bono y su rendimiento al vencimiento se relacionan de algunas maneras muy específicas. En el próximo análisis, demostraremos cuatro características importantes de esta relación:
- El precio y el rendimiento al vencimiento se relacionan inversamente.
- Cuando el rendimiento al vencimiento está por debajo de la tasa del cupón, el precio del bono estará por encima del valor nominal; es decir, el bono venderá a una prima.
- Cuando el rendimiento al vencimiento está por encima de la tasa del cupón, el precio del bono estará por debajo del valor nominal; es decir, el bono venderá a descuento.
- El precio y el rendimiento son convexos.
Podemos observar estas cuatro características en la Figura 3-1, que es una representación gráfica de la relación entre el Precio y el Rendimiento al Vencimiento para un bono a 10 años con una tasa de cupón de 7,0%.
En el eje vertical del gráfico medimos el precio del bono. En el eje horizontal, medimos el rendimiento al vencimiento del bono. Los puntos de los datos para la línea precio-rendimiento ilustrada en la Figura 3-1 son los que aparecen en la tabla 3-1, a continuación.
Figura 3-1 Relación precio-rendimiento para un bono a 10 años, con cupón 7,0%
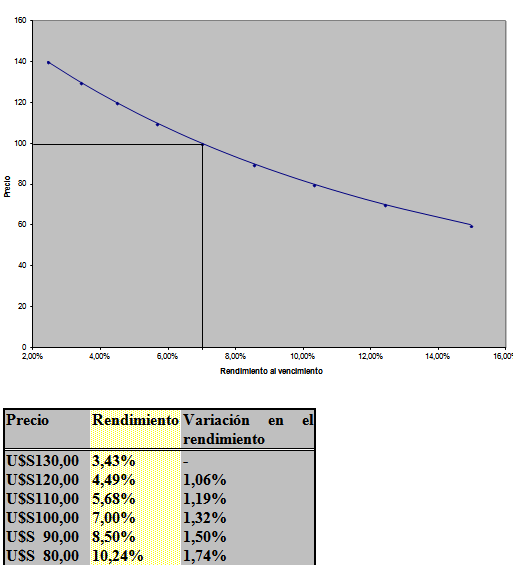
Tabla 3-1 Datos de precio-rendimiento para un bono a 10 años, con cupón 7,0%
La primera observación que se debes hacer es que la curva de la línea P-i es negativa. Es decir, cuando el rendimiento al vencimiento aumenta, el precio del bono cae. Esto también se puede observar en la tabla 3-1.
Cuando el precio del bono está en su valor nominal, U$S100, su rendimiento al vencimiento es igual a la tasa del cupón, 7,0%. Obsérvese lo que sucede al rendimiento al vencimiento cuando el precio sube a U$S110: el rendimiento cae a 5,68%.
Intuitivamente, si PV es superior al valor nominal del bono, dados los mismos pagos de cupón, la única manera de que la ecuación dé es si la tasa de descuento, i, es menor.
Por otro lado, si el PV es menor, dados los mismos pagos de cupón, la ecuación dará sólo si si la tasa de descuento, i, es mayor.
Para las características claves finales de los títulos de renta fija, refiérase nuevamente a la tabla 3-1. Vemos que por cada oscilación en el precio de U$S10, la oscilación correspondiente del rendimiento no es constante.
Por ejemplo, si el precio del bono cae de U$S130 a U$S120, el rendimiento al vencimiento aumenta un 1,06%. Si el precio del bono cae más aun de U$S120 a U$S110, el rendimiento al vencimiento aumenta un 1,19%.
(*) Dr. Juan Báez Ibarra – Máster y Doctor en Contabilidad por la Fundación Getulio Varga (FGV) y Universidad de San Pablo (USP) del Brasil, respectivamente. Instructor nacional e internacional de Riesgos Financieros, Productos y Mercados Financieros, NIIFs, ALD y Gestión Integral de Riesgos. Amplia experiencia en Entidades Financieras.