Juan Báez Ibarra (*)
Con este artículo completamos la revisión de los conceptos relacionados a la Estadística para calcular el VaR
Percentiles
Indica el valor que tiene la variable observada cuando se han acumulado un x% de observaciones colocadas en orden.
Distribución Normal
- Se dice que una distribución es normal (o se ajusta a una normal) cuando existe una alta probabilidad de que las observaciones se acerquen a la media y que la probabilidad sea simétricamente menor conforme se aleje de ella
- La Distribución Normal tiene la forma de una campana simétrica cuya media, mediana y moda coinciden en el mismo valor
- Es asintótica por naturaleza, pues nunca toca el eje horizontal
- La Distribución Normal puede ser descrita por dos datos, su media y su desviación estándar
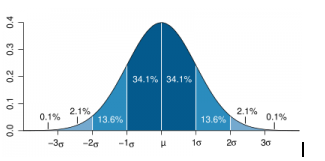
Distribución Normal Estándar
- Es aquella que tiene una media de 0 y distribución estándar de 1
- Las variables aleatorias pueden estar definidas en una variedad de unidades de medición: dólares, metros, minutos, etc.
- En el caso de la distribución normal estándar siempre son unidades estandarizadas (unidades de desviación estándar) y se representan en una sola distribución (valores z)
- Cualquier distribución Normal puede ser transformada a una distribución normal estándar, mediante la siguiente formula:
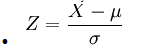
Donde:
Z es la unidad estandarizada de la desviación estándar calculada
X es el valor puntual de la variable observada
µ es la media de los valores de la variable observada
σ es la desviación estándar
Intervalos de Confianza
Relación directa entre desviación estándar e intervalos de confianza de la distribución
Intervalo de confianza de dos colas

Covarianza
- Es un indicador que mide el grado en el que dos variables se mueven en línea.
- Una covarianza positiva indica que las variables se mueven en la misma dirección (atraen) y si es negativa que se mueven en direcciones opuestas (repelen)
- La formula de la covarianza es la sumatoria del producto de las dispersiones de las dos variables dividido para el número de observaciones:
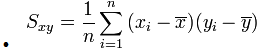
- No indica necesariamente que tan fuerte es la atracción entre las variables.
Coeficiente de Correlación
- Mide la fuerza y la dirección de una relación lineal entre dos variables aleatorias.
- Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos (coexistentes) de la otra.
- La correlación es un número entre +1 y -1
- No mide ni la volatilidad de alguna de las series ni indica necesariamente un sentido de causa y efecto.
- Se calcula utilizando la Correlación de Pearson: es la razón de dividir la covarianza de las dos variables para el producto de sus desviaciones estándar.
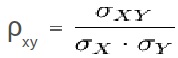
(*) Dr. Juan Báez Ibarra – Máster y Doctor en Contabilidad por la Fundación Getulio Varga (FGV) y Universidad de San Pablo (USP) del Brasil, respectivamente. Instructor nacional e internacional de Riesgos Financieros, Productos y Mercados Financieros, NIIFs, ALD y Gestión Integral de Riesgos. Amplia experiencia en Entidades Financieras.